
Solution: The key to solve the problem is to equate the drain flow rate to the level drop in the tank. But the trick is that the drain flow rate depends on the level.
Drain flow rate = cross-sectional area x velocity
=

Velocity is obtained by equating potential energy to kinetic energy as it is freely falling under gravity,

Rate of volume drop in the tank = cross-sectional area x rate of infinitesimal level drop in the tank
=

Equating both, we have


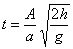
7 comments:
Comrade,
I did not understand the reasoning behind equating the potential and kinetic energies and least of all the justification that this is the case for all freely falling bodies.
Let us consider a typical mass at a height. Just before the fall it possesses maximum PE and as it falls it gains KE at the expense of PE until the former is max when the latter is zero. Only at one particular instant of motion can one say PE = KE.
Moreover, a fluid possess
- Pressure energy ( dens * g * h )
and
- datum energy ( hydraulic head p/ density )
why is Potential energy favored in the place of Pressure energy and why is datum head ignored.
I think we can safely do away with the question of how the energy of the fluid varies, to find a solution to this problem.
Also, we are in need of a MAJOR assumption
namely,
THE TANK IS OPEN AT THE TOP
. Only then can we claim the vel = sqrt(2gh)
Also I think its better to say that rate of efflux from the drain pipe = a* C * sqrt(2gh).
Where C is a discharge co-efficient.
Though you have ignored the use of 'C', I think theoretically it cannot be discarded. I think it has a value of 0.9 and hence explains why you ignored it. Right?
so,
-dV/dt = a*C*sqrt(2gh)
integrating both sides and solving for t the solution can be arrived at.
where,
V= A * h.
this will give the same result that you have obtained when the boundary conditions are applied. i.e V=A*h at t=0
and V=0 at t= T.
even in your solution the need to determine velocity does not arise.
1. The fluid flowing out under gravity (ignoring friction and viscosity) is the case of a freely falling body.
2. The various energies it possesses are i. static head, ii. dynamic head and iii. pressure head. Dens*g*h is static head and not pressure head. Dens*g*h is nothing bur potential energy. And in this case there is no pressure head.
And as friction and viscosity are ignored, flow coefficient can also be ignored. It unncessarily complicates simple things.
kya backwash hai ye blog viscosity area velocity and control valves ke liye nahi hai
da wer r did u get this data from??
in the final expression why 2 on th e numerator inside the root.. it shud b in the denomintr rite??...
mithun parameswaran
Post a Comment